Probability Theory

Due to uncertainty around us, we are talking about probability now. The cause of uncertainty is numerous ranging from noises to the limited data sizes. Probability Theory helps us by providing a consistent framework for the qualification and manipulation of the uncertainty and helps us get the foundation of pattern recognition.

There are two fundamental rules of probability theory viz;

• Sum rule
• Product rule

Sum Rule

To understand the sum rule, we will start with an example from Khan Academy.

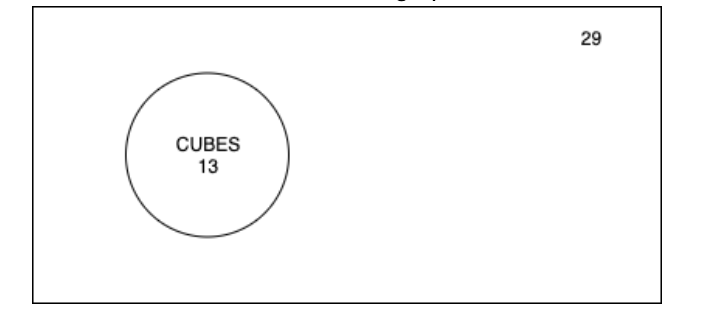
Suppose we have a bag with

• 8 Green Cubes
• 9 Green Spheres
• 5 Yellow Cubes
• 7 Yellow Spheres

So, what is the probability of getting a cube of any color, P(Cube of any color) ? Before answering the question let’s ponder on few things. There are altogether 29 objects in the bag and out of which 13 are the cubes. Let’s see in the graph below:

So, considering that each outcome form the bag is equally likeable(we assume this unless mentioned), the probability of getting cube of any color from the bag is:

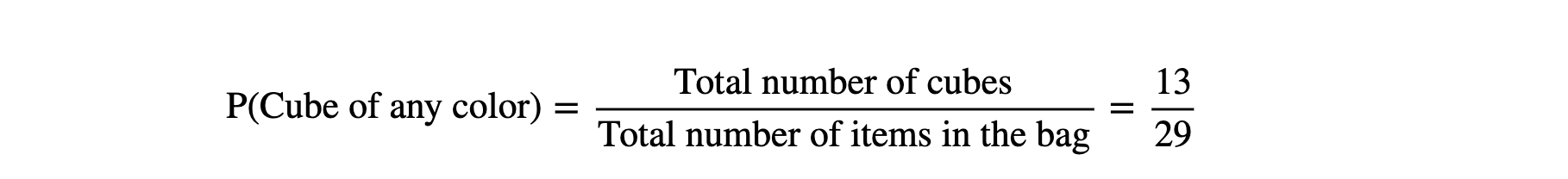
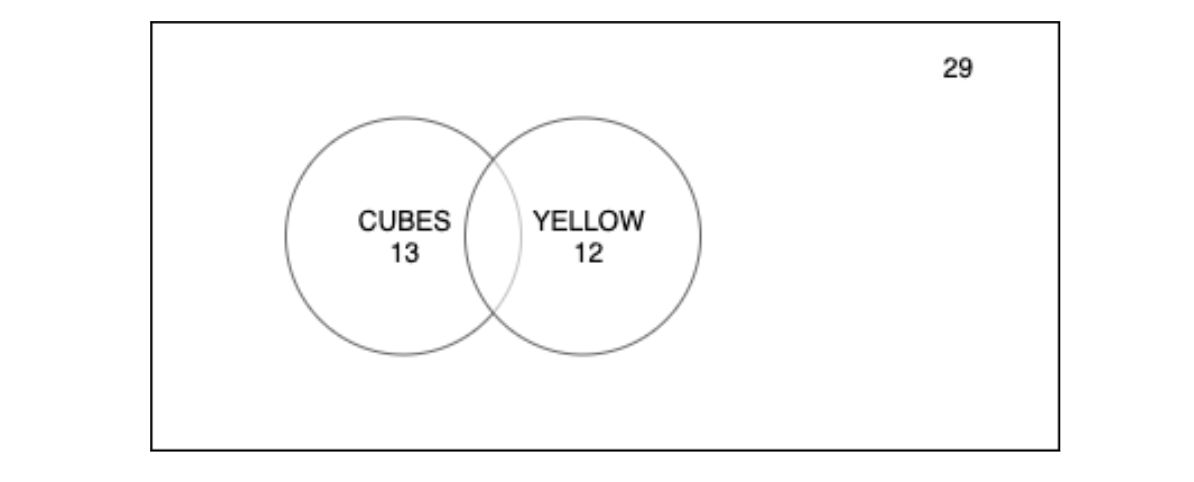
Similarly, let’s find out the probability of popping out a yellow item from the bag. There are altogether 12 items in the bag, comprising 5 yellow cubes and 7 yellow spheres. In diagram:

Again, considering the each item from the bag equally probable to pop out, the probability of getting yellow item is:

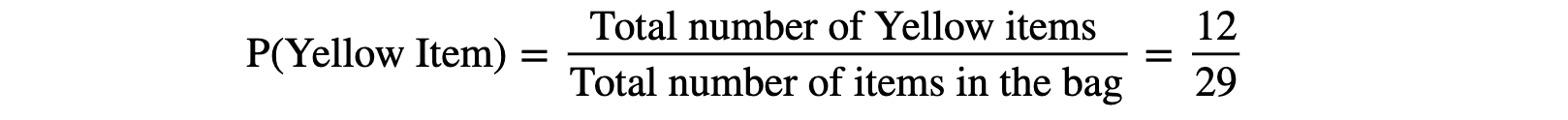
So, what is the probability of getting a yellow cube? Well, we have 29 equal possibilities and hence, the probability of getting a yellow cube is:

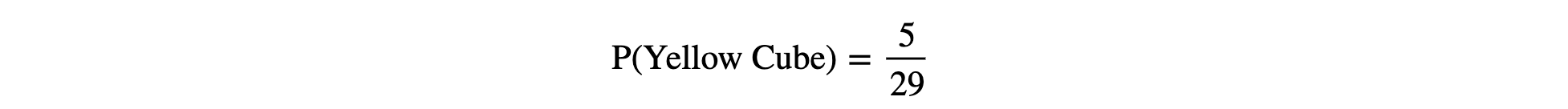
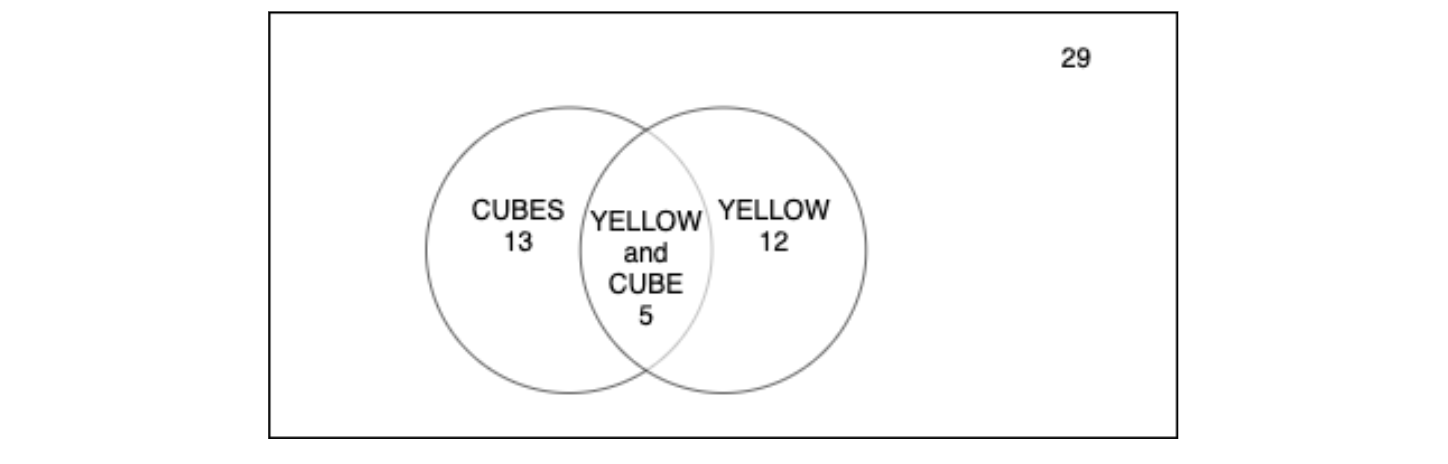
So, this thing can be easily verified and visualized through a Venn diagram. The intersection portion of the diagram comprises the 5 yellow cubes, i.e., both cubes and yellows. In diagram:

Now that we are warmed up with some of the basic probability values, it is the right time to ask a question, What is the probability of getting a yellow item or cube of any color? In notation:

P(Yellow item or Cube of any color)=?

Now, we will take help from the Venn diagram. The denominator is 29, for sure, since there are total items as 29 and they are equally likely to pop put. For the numerator part, we need to encounter both yellow items and cubes. So, the total yellow items are 12 and the total 13 cubes. But remember that while considering 12 yellow items, we have already taken 5 yellow cubes into account, which is given by the intersection section of the Venn diagram. Hence,

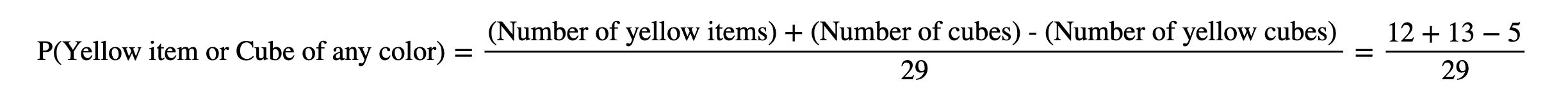
So, we removed the hidden 5 yellow cubes under the yellow items because we have already taken total cubes into account. Now, we can replace these above numbers in probability terms as:

In General,

P(A or B)=P(A)+P(B)−P(A and B)

This is called the Addition rule. We can’t just add two probabilities, because they might have some overlapping and we have to encounter them by subtraction. In case, if we don’t have an overlap as in the diagram below, the intersection would be 0 and this would be simply adding the probabilities, i.e.,

P(A or B)=P(A)+P(B) since, P(A and B) = 0

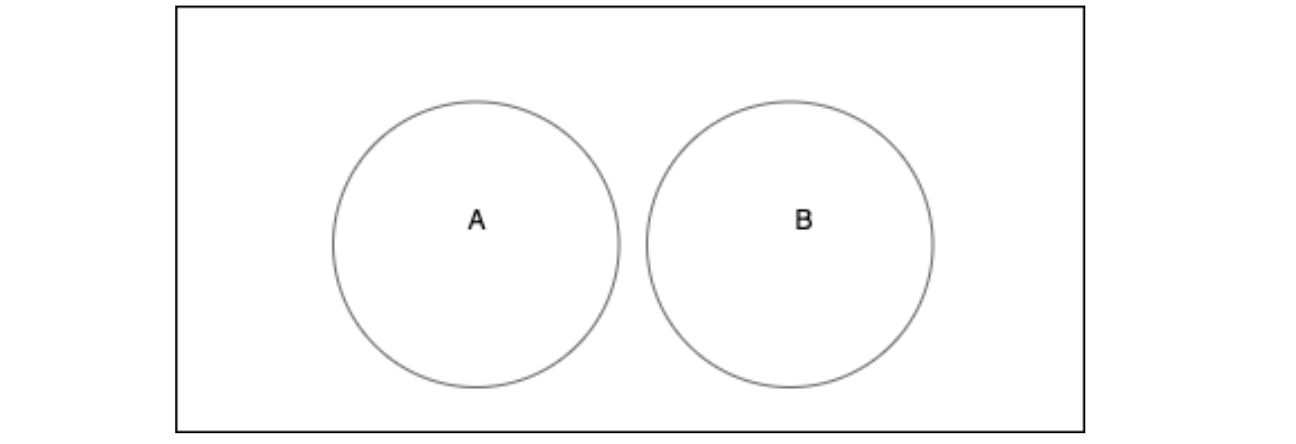
In addition, such events are called mutually exclusive, since event A and event B can’t happen at the same time. Occurrence of event A implies the non-occurance of event B.

Now, we will see another fundamental rule of the probability, the Product Rule.

Product Rule

For the product rule, we will start with the formula and then interpret its meaning. But first, we will talk about the two types of events:

• Independent Events
• Dependent Events

Probability is all about determining the likelihood of the events.

Independent Events

Two or more events are called independent if the occurrence of one event doesn’t affect the occurrence of any other events. For example probability of getting one on a first roll and then three in the second roll in a normal six-sided dice, because both events are independent of each other and have the probability of 1/6 .

Dependent Events

Two or more events are called dependent if the occurrence of one event affects the occurrence of other events. For example probability of getting an Ace in drawing the first card from a deck of the 52 cards and then getting a King in drawing the second card from the remaining 51 cards.

These events are dependent because drawing an Ace changes the probability of getting King in the second place since the sample spaces decrease from 52 to 51.

So, now we know the definition of Independent events and dependent events, let’s proceed to the product rule. We have a product rule for both independent and dependent events.

A question to start: What is the probability of rolling 3 and then 1 on normal six-sided dice? Since these are independent events, we will use the product rule for independent events, i.e.,

P(getting three on first roll and getting one on second roll)=P(getting three on first roll)∗P(getting one on the second roll)

P(getting three on first roll and getting one on second roll)=1/6∗1/6=1/36

Generally for the two independent events, 𝐴 and 𝐵 , the multiplication(Product rule, AND rule) states:

P(A and B)=P(A)∗P(B)

Let’s consider a different scenario.

Consider drawing two cards from a deck of 52 cards. What is the probability of getting a red card on the first draw and then getting again a red card on the second draw without replacement?

Our of 52 cards in a deck, 26 cards are red so the probability of getting a red card in the first draw is 26/52 or 1/2 . But the probability of getting a red card in the second draw no longer remains 26/52 . Since the number of the total cards is decreased to 51 .

This is an example of dependent events. Now, we will see, how the probabilities are affected in the case of dependent events.

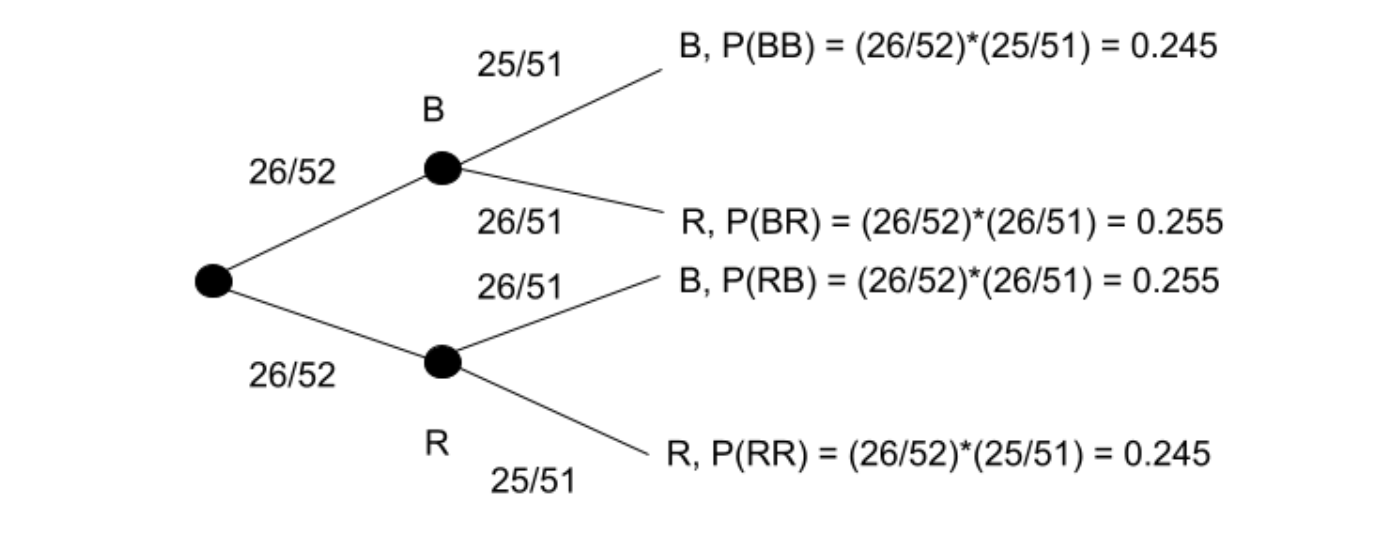
Hence, from the tree diagram, we know that the probability of getting red cards on both draws is:

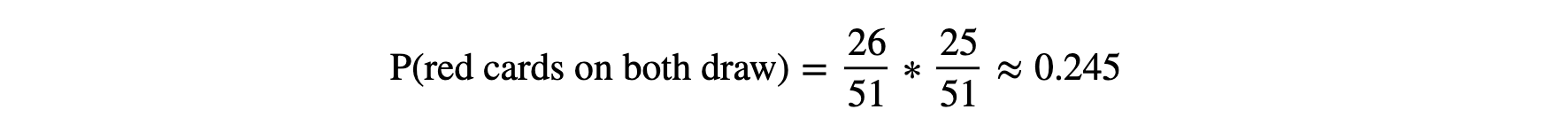
Now, let’s generalize this experiment to the universally known Probability rule or multiplicative rule of probability.

For any two events, we can say that:

P(A and B)=P(A)∗P(B|A)

Here, the term P(A|B) is to be understood carefully. The vertical bar is read as “given”. So, P(A|B) is the “probability of occurring A given than A has already occurred”. This is often known with the name of Conditional Probability.

In our former example of drawing cards, we can see the implementation of this formula.

P(A) = P(Red card in first draw)

P(B) = P(Red card in second draw)

P(A and B) = P(Red card in first draw and Red card in second draw) = P(A)*P(B|A)

Here in this case, P(B|A) = P(Red in the second draw given that Red is in the first draw)

Since we know, P(A) = P(Red card in first draw) =26/52

P(B|A) = P(Red in second draw given that Red is in first draw) =25/51

P(A and B) = P(A)*P(B|A)=(26/52)∗(25/51)≈0.245

To sum up, the product rule says that we can multiply the probabilities of two events to get the probability of occurrence of both events, but we need to take the first event into account when considering the probability of the second event, in case the events are dependent. In the case of independent events,when the occurrence of one event doesn’t impact the probability of the other,

𝑃(B|A)=𝑃(𝐵)

and hence the product rule turns out to be:

P(A and B) = P(A)*P(B)